La regresión lineal es un método estadístico utilizado para modelar la relación lineal entre una variable dependiente y una o más variables independientes. Es un método ampliamente utilizado en el análisis de datos y tiene una variedad de aplicaciones en una amplia gama de campos, como la economía, las finanzas y las ciencias sociales.
En la regresión lineal, la relación entre las variables se modela mediante una ecuación lineal de la forma:
donde y es la variable dependiente, x1, x2, ..., xn son las variables independientes y b0, b1, b2, ..., bn son los coeficientes o pesos que representan la fuerza y la dirección de la relación entre las variables.
Hay varios tipos de regresión lineal, incluyendo la regresión lineal simple, que implica modelar la relación entre una sola variable independiente y una variable dependiente, y la regresión lineal múltiple, que implica modelar la relación entre múltiples variables independientes y una variable dependiente.
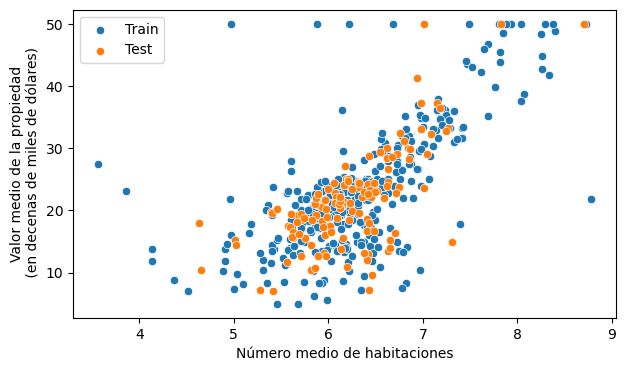
La regresión lineal tiene una serie de aplicaciones, incluyendo:
-
Predicción de un resultado continuo: la regresión lineal se puede utilizar para predecir un resultado continuo, como el precio de una acción o la demanda de un producto, en función de una o más variables independientes.
-
Evaluación de la fuerza y dirección de la relación entre las variables: la regresión lineal se puede utilizar para determinar la fuerza y dirección de la relación entre las variables, lo que puede ser útil para entender los factores subyacentes que influyen en la variable dependiente.
-
Identificación de los predictores más importantes: la regresión lineal se puede utilizar para identificar los predictores más importantes de una variable dependiente, lo que puede ser útil para identificar los factores clave que impulsan un resultado determinado.
En general, la regresión lineal es una herramienta estadística poderosa que tiene una amplia gama de aplicaciones en diversos campos. Es un método simple y efectivo para modelar la relación entre una variable dependiente y una o más variables independientes y se puede utilizar para hacer predicciones, evaluar relaciones y identificar predictores importantes.