La Descomposición en Valores Singulares (SVD, por sus siglas en inglés, Singular Value Decomposition) es una potente técnica matemática que se utiliza para descomponer una matriz en sus partes constituyentes. Es una generalización de la descomposición en autovalores de una matriz, y se puede aplicar a cualquier matriz rectangular, no solo a las matrices cuadradas.
La descomposición de una matriz A en su SVD viene dada por la ecuación A = UΣVT, donde U y V son matrices ortogonales y Σ es una matriz diagonal con los valores singulares de A en la diagonal.
Por ejemplo, consideremos la siguiente matriz A:
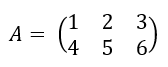
La SVD de A se puede calcular como:
donde:

La matriz U está compuesta por los vectores singulares izquierdos de A, la matriz Σ está compuesta por los valores singulares de A, y la matriz VT está compuesta por los vectores singulares derechos de A.
La SVD tiene muchas aplicaciones en álgebra lineal y análisis numérico, tales como:
-
Compresión de datos: Al mantener solo los mayores valores singulares y los vectores singulares correspondientes izquierdos y derechos, podemos reducir la dimensionalidad de los datos preservando la mayor parte de la información.
-
Pseudoinversa: La pseudoinversa de una matriz se puede calcular utilizando SVD, lo cual es útil para resolver ecuaciones lineales con una matriz no cuadrada.
-
Análisis de componentes principales (PCA, por sus siglas en inglés): PCA es una técnica de reducción de dimensionalidad que utiliza SVD para encontrar los componentes principales de un conjunto de datos.
-
Análisis semántico latente (LSA, por sus siglas en inglés): LSA es una técnica utilizada en procesamiento del lenguaje natural que utiliza SVD para encontrar patrones subyacentes en grandes corpora de texto.
-
Sistemas de recomendación: SVD se utiliza en sistemas de recomendación para reducir la dimensionalidad de los datos y encontrar características latentes que se pueden utilizar para hacer recomendaciones.
En resumen, la SVD es una potente técnica matemática que tiene muchas aplicaciones en álgebra lineal y análisis numérico, incluyendo la compresión de datos, la pseudoinversa, el análisis de componentes principales, el análisis semántico latente y los sistemas de recomendación.