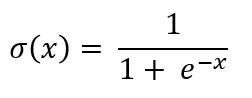La neurona de Frank Rosenblatt, como ya sabemos, aplicaba una función escalón al resultado de la suma del producto escalar de los valores de entrada y los pesos, y el bias. Tal y como veremos más adelante, el uso de la función escalón suponía importantes limitaciones que tardaron en ser resueltas.
Una de la primeras funciones de activación que se usaron para sustituir a la función escalón fue la sigmoide, función definida por la siguiente expresión:
...y que podemos representar de la siguiente forma:
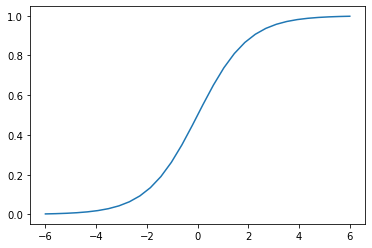
Comprobamos que, para valores muy negativos de x, la función tiende al valor 0, y que, para valores muy positivos de x, la función tiende al valor 1.
Si, tal y como hemos visto, la entrada a la función de activación (el resultado al que hemos llamado "z" en una sección anterior) viene dada por la expresión "w•x + b", la neurona sigmoide devolverá el resultado de aplicar la función sigmoide a este valor, es decir:
salida = σ(w•x + b)
El esquema de este tipo de neuronas es, por lo tanto, el siguiente:
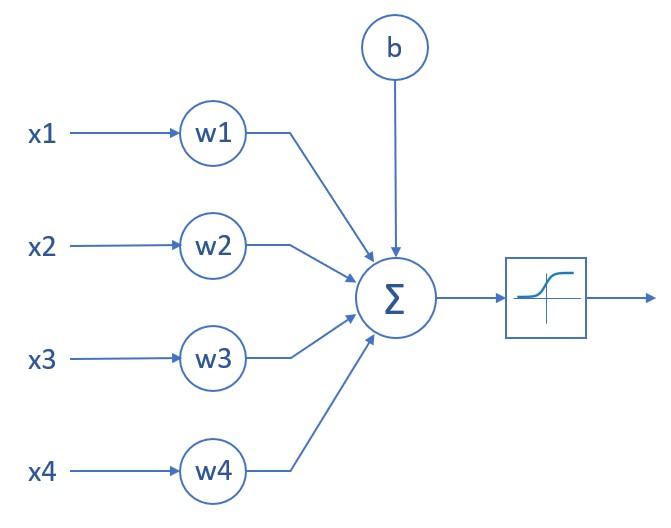
...siendo el único cambio con respecto al último esquema visto la sustitución de la función escalón por una función sigmoide.