Además de la elección correcta del parámetro k, otro aspecto crítico a decidir es el concepto de distancia a considerar. En los ejemplos vistos hasta ahora se ha considerado como distancia entre dos puntos la distancia euclidea (es decir, la distancia "ordinaria" entre dos puntos en un espacio euclideo). En un espacio de estas características de dos dimensiones (en un plano), la distancia entre dos puntos P1 y P2 de coordenadas (x1, y1) (x2, y2) viene dada por el teorema de Pitágoras:
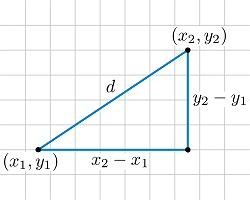
De esta forma, cuando nos referimos a los 3 vecinos más próximos, por ejemplo, estamos haciendo referencia a los tres puntos cuya distancia (en el sentido clásico) es menor. Si estamos trabajando en un espacio de dos dimensiones, parece claro que los tres puntos cuyas coordenadas se muestran a continuación están relativamente cerca unos de otros:
| x | y |
|---|---|
| 3 | 4 |
| 4 | 2 |
| 3 | 3 |
...al menos si los comparamos con los dos siguientes puntos que, aunque están próximos entre sí, distan bastante de los tres puntos anteriores:
| x | y |
|---|---|
| 32 | 15 |
| 31 | 17 |
Trabajando en un espacio de, digamos, cinco dimensiones (un conjunto de datos con cinco características), los siguientes puntos podrían considerarse próximos:
| c1 | c2 | c3 | c4 | c5 |
|---|---|---|---|---|
| 4 | 3 | 5 | 7 | 2 |
| 3 | 3 | 4 | 6 | 2 |
| 4 | 2 | 6 | 7 | 2 |
| 4 | 3 | 4 | 7 | 3 |
...mientras que los siguientes puntos están próximos entre sí pero no parecen cerca de los anteriores (compárese los valores de las características c1 o c5, por ejemplo):
| c1 | c2 | c3 | c4 | c5 |
|---|---|---|---|---|
| 7 | 2 | 3 | 4 | 6 |
| 8 | 3 | 2 | 5 | 8 |
| 7 | 3 | 2 | 4 | 7 |
| 7 | 2 | 2 | 4 | 7 |
Este concepto de "parecido" o "proximidad" es bastante intuitivo y funciona bien en muchas circunstancias. Pero no en todas. Veamos un par de casos...