Y volviendo al entrenamiento del Perceptrón, pongamos un ejemplo del proceso a seguir. Veíamos que los datos de entrenamiento eran:
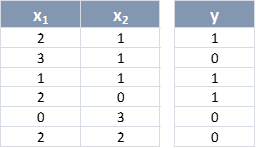
Y recordemos que el valor resultante del sumatorio, z, tenía la siguiente expresión:
Supongamos que los pesos se inicializan con los valores w0 = 0, w1 = -1, w2 = 1 y escogemos una tasa de aprendizaje de 0.1 (estos valores no son muy reales, pero nos sirven para entender el proceso). Pasaríamos la primera muestra x(1) = (2, 1):
Es decir, se obtiene un valor menor que 0, lo que supone que la neurona no se va a activar y devolverá un valor ŷ = 0, aun cuando la etiqueta asociada a esta muestra es 1. Si calculamos los incrementos a aplicar a cada peso:
Δw0 = η(y – ŷ).x0 = 0.1*(1 – 0)*1 = 0.1
Δw1 = η(y – ŷ).x1 = 0.1*(1 – 0)*2 = 0.2
Δw0 = η(y – ŷ).x2 = 0.1*(1 – 0)*1 = 0.1
Por lo que los pesos quedarían ahora con los siguientes valores:
w0 = w0 + Δw0 = 0 + 0.1 = 0.1
w1 = w1 + Δw1 = -1 + 0.2 = 0.8
w2 = w2 + Δw2 = 1 + 0.1 = 1.1
Vemos que los pesos se han modificado un poco de forma que la neurona tienda a un estado en el que obtener la etiqueta correcta para la muestra x(1) sea un poco más probable. Y, tal y como se ha comentado, la velocidad del cambio de los pesos viene determinada por la tasa de aprendizaje, η.
Si la predicción realizada por la neurona, ŷ, hubiese coincidido con la etiqueta de la muestra, y, los incrementos a aplicar a los pesos hubiesen sido igual a cero.