Se ha comentado que el proceso seguido por el árbol de decisión se basa en la idea de separar los datos de forma que se mejore la pureza de los bloques resultantes. Esta mejora es la que se mide mediante la llamada ganancia de información (information gain o IG en inglés), definida mediante la siguiente fórmula:
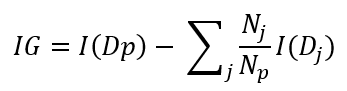
En la que:
- I es la función que mide la impureza
- Dp es el dataset "padre" que se está dividiendo
- Np es el número de elementos del dataset padre
- Dj es el dataset j-ésimo en el que se ha dividido Dp
- Nj es el número de elementos del dataset Dj
Básicamente estamos restando a la impureza del dataset inicial la impureza de los bloques resultantes ponderados según su número de elementos con respecto al total.
Si estamos trabajando en un escenario de clasificación binaria, la función anterior queda:
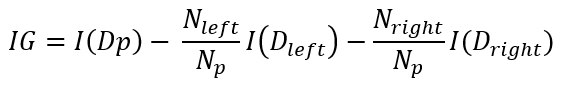
En este caso Dleft es uno de los dos bloques resultantes de la división (y Nleft su número de elementos) y Dright el segundo bloque (y Nright su número de elementos).
Ésta es la función objetivo que se desea maximizar en cada "split" buscando la característica adecuada por la que realizar la división y el umbral adecuado.
Pongamos un ejemplo: supongamos que el dataset padre contiene 90 muestras y una impureza medida vía Índice Gini de 0.4. Este dataset se divide en dos grupos de 60 y 30 elementos, cuyas impurezas son 0.2 y 0.5 respectivamente. La ganancia de información sería:
IG = 0.4 - 60/90 * 0.2 - 30/90 * 0.5 = 0.1