Si quisiéramos comparar los resultados devueltos por las tres funciones para un escenario de clasificación binaria, podríamos hacerlo de la siguiente forma:
x = np.linspace(0.001, 0.999, 1000)
gini = 1 - x ** 2 - (1 - x) ** 2
entropy = - x * np.log2(x) - (1 - x) * np.log2(1 - x)
error = 1 - np.maximum(x, 1- x)
gini = 1 - x ** 2 - (1 - x) ** 2
entropy = - x * np.log2(x) - (1 - x) * np.log2(1 - x)
error = 1 - np.maximum(x, 1- x)
fig, ax = plt.subplots()
ax.plot(x, gini, label = "Índice Gini")
ax.plot(x, entropy, label = "Entropía")
ax.plot(x, error, label = "Índice de error")
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("p")
ax.set_ylabel("Impureza")
ax.legend()
plt.show()
ax.plot(x, gini, label = "Índice Gini")
ax.plot(x, entropy, label = "Entropía")
ax.plot(x, error, label = "Índice de error")
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("p")
ax.set_ylabel("Impureza")
ax.legend()
plt.show()
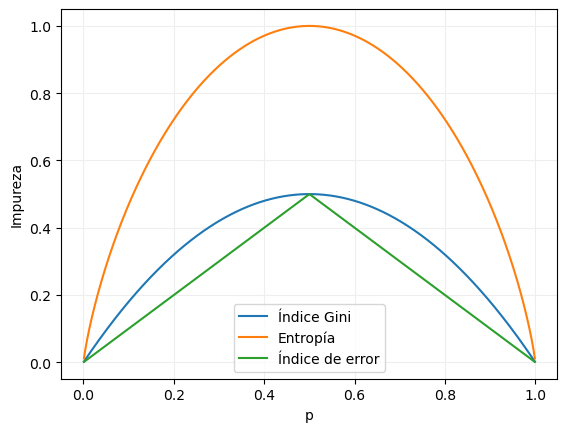
Vemos que, aparte de la diferencia de escala, la naturaleza de las tres funciones es semejante, devolviendo un valor máximo cuando ambas clases están igualmente representadas, y un valor mínimo cuando la proporción de una de las clases es 0 o 1.
En la práctica, el índice Gini y la entropía devuelven resultados muy similares.