Por último, el índice de error o error de clasificación se calcula con la siguiente fórmula:
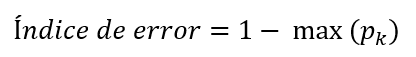
Es decir, es la clase mayoritaria (aquella con la mayor proporción de elementos) la que establece el error. En un escenario de clasificación binaria, la expresión anterior queda reducida a:
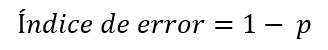
Siendo p, en este caso, la proporción de la clase mayoritaria.
En nuestro ejemplo, la mayor proporción viene dada por la clase 0 (recordemos que era la clase con 3 muestras), por lo que:
error de clasificación = 1 - 3/5 = 0.4
Podemos representar esta función de impureza en un escenario de clasificación binaria con el siguiente código:
x = np.linspace(0, 1, 100)
y = 1 - np.maximum(x, 1- x)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("p")
ax.set_ylabel("Índice Gini")
plt.show()
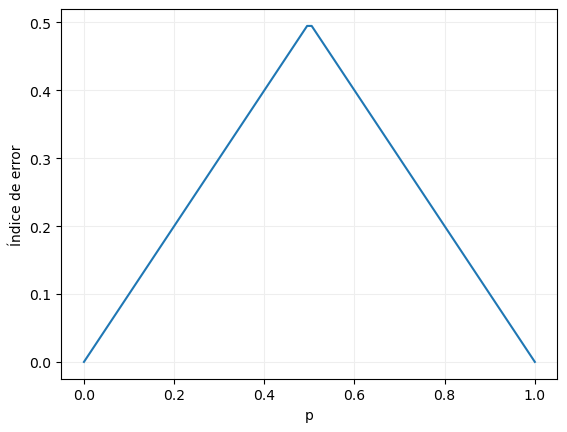
También aquí la función tiene su máximo cuando las dos clases están igualmente representadas en el dataset, en cuyo caso toma el valor 0.5.