Support Vector Machines, SVM (Máquinas de Vectores de Soporte en español) son un conjunto de versátiles y potentes algoritmos desarrollados en los laboratorios AT&T, útiles tanto en escenarios de clasificación como de regresión.
La idea detrás de SVM es la siguiente (en un escenario sencillo e ideal): Partimos de un conjunto de puntos en un plano que pertenecen a dos clases distintas:

El objetivo es encontrar una recta (un hiperplano, en general) que permita separar ambos bloques de puntos. En el caso mostrado en la imagen anterior, existe un número infinito de rectas candidatas a resolver el problema:
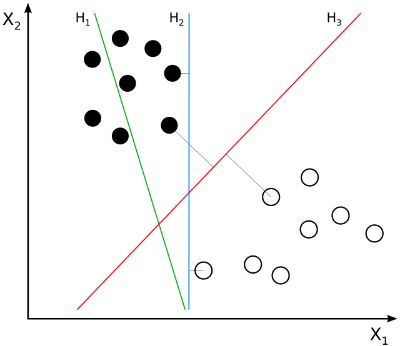
En la imagen anterior, la recta H1 no divide correctamente los dos bloques (pues ni siquiera está clasificando correctamente los puntos negros). La recta H2 sí lo hace, pero su proximidad a los puntos negros hace que difícilmente pueda generalizarse el resultado (puede existir en el conjunto de puntos sobre los que realizar la predicción alguno que quede cerca de los puntos negros pero a la derecha de la recta H2, siendo, por lo tanto, mal clasificado).
La recta H3, desde cierto punto de vista, es la recta ideal, pues maximiza la distancia mínima a los puntos negros y blancos, optimizando la capacidad de generalización del algoritmo:
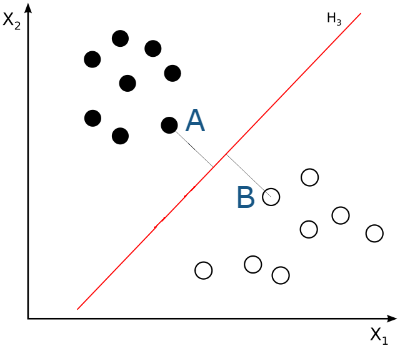
(Imágenes anteriores extraídas de la wikipedia y modificadas convenientemente).
Los puntos A y B, los más próximos a la recta H3, son los que determinan la posición de la recta. Si esta recta existe (si los puntos son linealmente separables) se denomina hiperplano de máximo margen (maximum-margin hyperplane), y los puntos A y B se denominan vectores de soporte (support vectors). La suma de las distancias que separan los puntos A y B del hiperplano de máximo margen se denomina margen.