Sin embargo, los puntos a clasificar no siempre van a ser linealmente separables. Si, por ejemplo, estamos trabajando en un espacio unidimensional, para los siguientes puntos no existe un hiperplano (un punto en este caso) que separe los puntos azules de los naranjas:
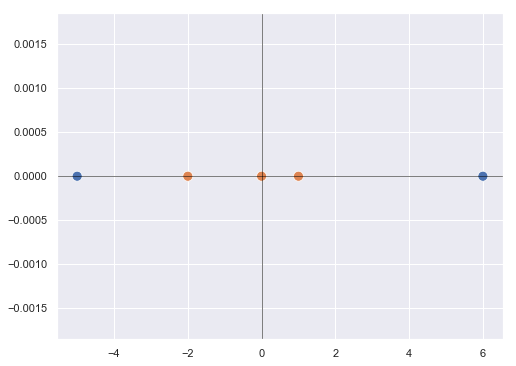
Pero ¿qué ocurriría si transformásemos estos puntos de forma que los situásemos en un espacio de mayor dimensionalidad tras aplicarles una cierta función? Por ejemplo, podemos llevar estos puntos (en un espacio de una dimensión) a un plano (espacio de dos dimensiones) de forma que su nueva coordenada x sea la misma coordenada x que tienen en el espacio original, pero que su coordenada y sea igual al cuadrado de su coordenada x. Los valores x iniciales de los puntos mostrados son:
-5, -2, 0, 1, 6
...y, tras aplicarles la transformación comentada, los valores y finales serían:
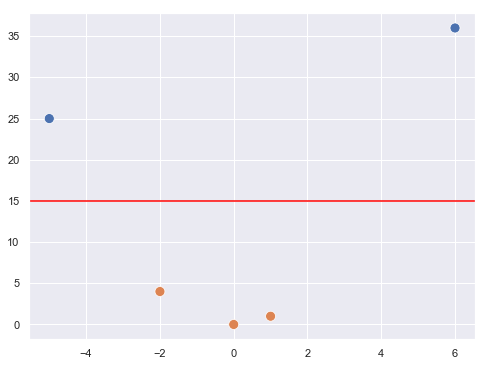
En el nuevo espacio, tal y como vemos en la imagen anterior, sí es posible crear una recta que separe ambos grupos de puntos, por el ejemplo la recta roja que se muestra (hay un infinito número de ellas, de hecho). SVM buscaría la recta que maximizase la distancia a ambos grupos de puntos en este nuevo espacio:
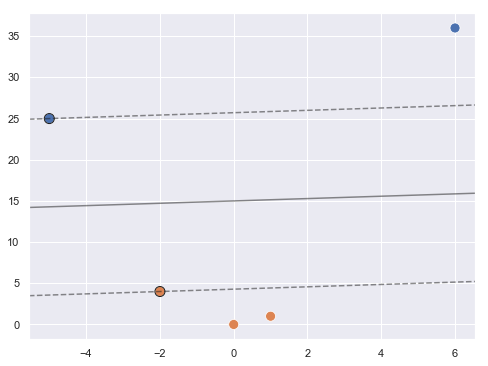
En la imagen anterior podemos distinguir el hiperplano de máximo margen (línea negra continua) y los vectores de soporte (bolas azul y naranja con borde negro). Para realizar una predicción sobre una muestra cualquiera, bastaría con aplicarle la misma transformación y ver a qué lado del hiperplano de máximo margen cae: si cayese por encima, se predeciría una bola azul. Si cayese por debajo, se predeciría una bola naranja.
Nótese que la posición del hiperplano de máximo margen queda determinada exclusivamente por los vectores de soporte (por los puntos más próximos al hiperplano): el tener más o menos puntos (además de los vectores de soporte) es irrelevante (siempre que no queden más cerca del hiperplano que los actuales vectores de soporte, por supuesto).
Esta transformación de las muestras desde el espacio original hasta una espacio de mayor dimensionalidad es llamada "kernel trick" (truco del kernel).