Transformemos nuestros datos de esta forma. Comenzamos importando la clase PolynomialFeatures e instanciándola:
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(2)
Antes de la transformación, nuestros datos tienen el siguiente aspecto:
X[:5]
array([[ 0.48813504],
[ 2.15189366],
[ 1.02763376],
[ 0.44883183],
[-0.76345201]])
A continuación, transformamos los datos:
X_poly = poly.fit_transform(X)
Ahora, los datos transformados tienen el siguiente aspecto:
X_poly[:5]
array([[ 1. , 0.48813504, 0.23827582],
[ 1. , 2.15189366, 4.63064634],
[ 1. , 1.02763376, 1.05603115],
[ 1. , 0.44883183, 0.20145001],
[ 1. , -0.76345201, 0.58285897]])
Obsérvese cómo, por ejemplo, el primer dato del dataset original (0.48813504) se ha transformado en la tripleta [1, 0.48813504, 0.488135042] (el cuadrado de 0.48813 es 0.23827, redondeando las cifras).
Ahora ya podemos instanciar un modelo de regresión lineal y entrenarlo:
model = LinearRegression()
model.fit(X_poly, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
normalize=False)
Veamos el resultado de la curva obtenida:
model.intercept_, model.coef_
(array([3.34050076]), array([[0. , 1.48743931, 0.48192376]]))
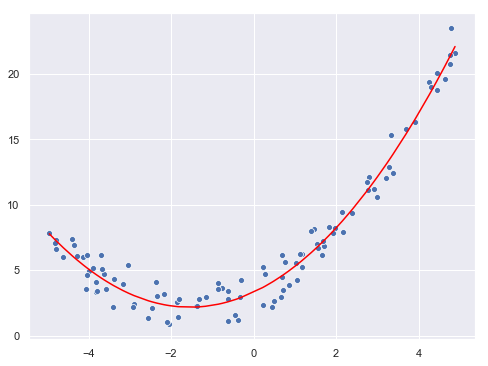
La curva original (sin contar con el ruido gaussiano introducido) tenía la forma 0.5x2 + 1.5x + 3. El resultado obtenido es (redondeando) 0.48x2 + 1.49x + 3.34. Realicemos la predicción de los puntos originales y mostrémosla en la gráfica:
prediction = model.predict(X_poly)
fig = plt.figure(figsize = (8, 6))
sns.scatterplot(x = X.flatten(), y = y.flatten());
sns.lineplot(x = X.flatten(), y = prediction.reshape(-1, ), color = "red");