La entropía utiliza la siguiente función para el cálculo de la impureza de un conjunto de datos:
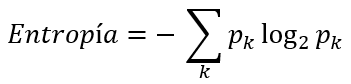
En un escenario de clasificación binaria, esta expresión queda reducida a:
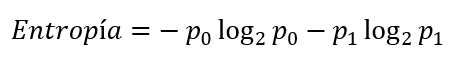
O, expresando la probabilidad p1 en función de p0:
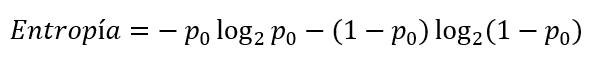
En el ejemplo que estamos viendo, la entropía tomaría el siguiente valor:
entropía = - p0 * log2(p0) - p1 * log2(p1) = - 3/5 * log2(3/5) - 2/5 * log2(2/5) = 0.9709
Podemos visualizar la distribución de la entropía en un escenario de clasificación binaria en función de la proporción de una de las clases con el siguiente código:
y = - x * np.log2(x) - (1 - x) * np.log2(1 - x)
ax.plot(x, y)
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("p")
ax.set_ylabel("Entropía")
plt.show()
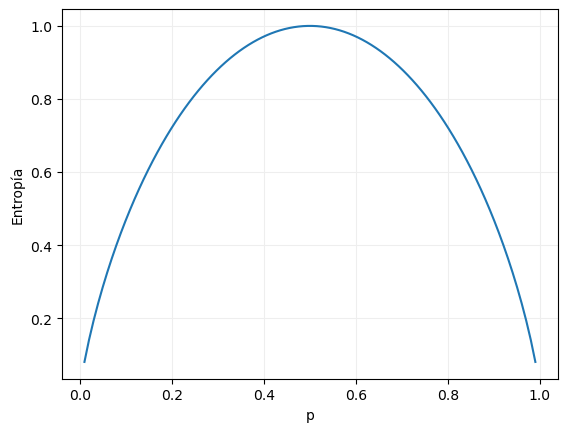
Por supuesto, el valor máximo de la entropía se da cuando la proporción de ambas clases es la misma (0.5), caso en el que la entropía toma el valor 1.
Y, al igual que se comentó para el índice Gini, la entropía toma el valor 0 cuando la proporción de la clase considerada sea igual a 0 o a 1, casos en los que solo habrá muestras de una única clase.
Y, también en este caso, el valor máximo de la entropía depende del número de clases. Si tenemos cuatro clases, por ejemplo, este valor sería de:
- 0.25 * log2(0.25) - 0.25 * log2(0.25) - 0.25 * log2(0.25) - 0.25 * log2(0.25) = 2