Singular Value Decomposition (SVD) is a powerful mathematical technique that is used to decompose a matrix into its constituent parts. It is a generalization of the eigendecomposition of a matrix, and it can be applied to any rectangular matrix, not just square matrices.
The decomposition of a matrix A into its SVD is given by the equation A = UΣVT, where U and V are orthogonal matrices and Σ is a diagonal matrix with the singular values of A on the diagonal.
For example, consider the following matrix:
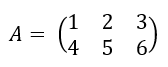
The SVD of A can be computed as:
where:

The matrix U is composed of the left singular vectors of A, the matrix Σ is composed of the singular values of A, and the matrix VT is composed of the right singular vectors of A.
SVD has many applications in linear algebra and numerical analysis, such as:
-
Data compression: By keeping only the largest singular values and corresponding left and right singular vectors, we can reduce the dimensionality of the data while still preserving most of the information.
-
Pseudoinverse: The pseudoinverse of a matrix can be calculated using SVD, which is useful for solving linear equations with a non-square matrix.
-
Principal component analysis (PCA): PCA is a dimensionality reduction technique that uses SVD to find the principal components of a dataset.
-
Latent semantic analysis (LSA): LSA is a technique used in natural language processing that uses SVD to find underlying patterns in large text corpora.
-
Recommender systems: SVD is used in recommender systems to reduce the dimensionality of the data and find latent features that can be used to make recommendations.
SVD is a powerful mathematical technique that has many applications in linear algebra and numerical analysis, including data compression, pseudoinverse, principal component analysis, latent semantic analysis, and recommender systems.