Siguiendo con nuestro ejemplo de la recta de regresión definida por los parámetros a y b:
habíamos decidido utilizar como función de coste el error cuadrático medio (llamémoslo "error" para simplificar), y habíamos visto que, para cada par de valores a y b, obtendríamos un error diferente. Imaginemos ahora que generamos muchas parejas de valores (a, b), tomando a y b valores entre, por ejemplo, -30 y 30, que calculamos el error correspondiente a cada combinación, y que mostramos el resultado en una gráfica de tres dimensiones en la que los valores de a y b se muestran en el plano horizontal y el error correspondiente se muestra en el eje vertical. El resultado -en un caso general- podría ser el siguiente:
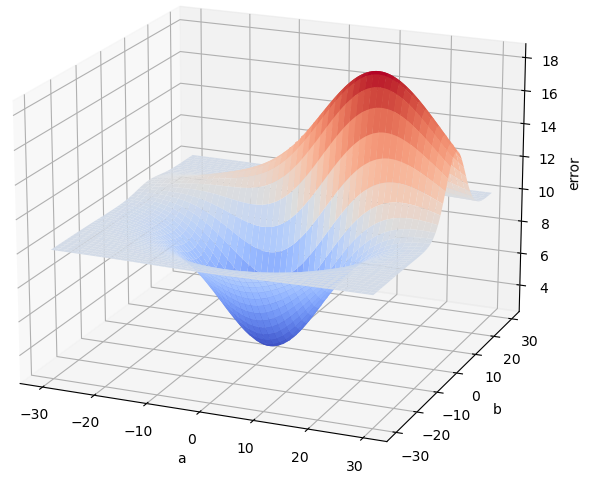
Vemos que hay una combinación de valores a y b que generan el menor error posible, y, aproximadamente, parece que está cerca de a = 0 y b = 0. La imagen anterior está creada a partir de datos de prueba -no tiene nada que ver con el error cuadrático medio de la recta que se ha puesto de ejemplo, pero nos sirve para explicar algunos conceptos. Así que supongamos que esta gráfica es la correspondiente a la recta.
El objetivo, una vez más, es averiguar la combinación de a y b para la que el error toma el valor más bajo posible. Y se ha comentado que al método usado para encontrar este mínimo lo denominamos optimizador (en Scikit-Learn el parámetro correspondiente recibe el nombre de solver).
Podríamos decantarnos, simplemente, por tomar valores aleatorios de a y b y quedarnos con la combinación que devolviese el error más bajo. Probablemente no encontraríamos el mínimo de la función de error, pero sería un posible método. Afortunadamente hay alternativas un poco más sofisticadas que devuelven resultados mucho mejores. Veamos algunas...