El índice Gini se calcula con la siguiente expresión:
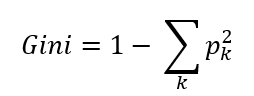
En el caso de un escenario de clasificación binaria, la fórmula queda reducida a la siguiente expresión:
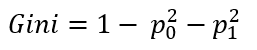
En el ejemplo comentado de 5 muestras, 3 de clase 0 y 2 de clase 1, el índice Gini sería:
Gini = 1 - 0.62 - 0.42 = 0.48
Podemos mostrar la distribución del índice Gini en función de la probabilidad de una de las clases con el siguiente código:
x = np.linspace(0, 1, 100)
y = 1 - x ** 2 - (1 - x) ** 2
fig, ax = plt.subplots()
ax.plot(x, y)
ax.grid(color = "#EEEEEE", zorder = 0)
ax.set_xlabel("p")
ax.set_ylabel("Índice Gini")
plt.show()
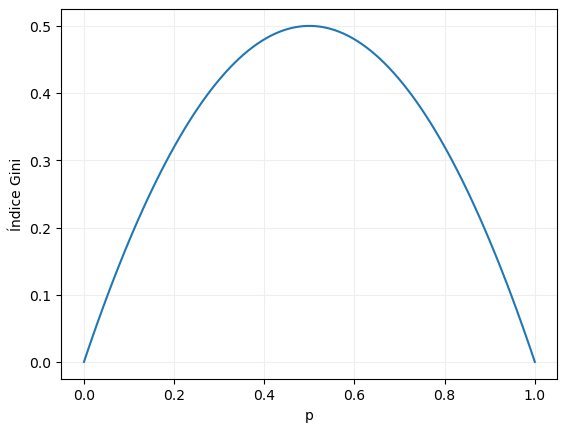
Es decir, la función toma valores próximos a cero cuando la proporción p de una de las clases es muy pequeña (lo que implica que el conjunto de valores está muy ordenado, pues si hay pocos elementos de la clase considerada significa que hay muchos de la otra clase) o cuando es muy grande (lo que implica, nuevamente, que hay pocos elementos de la otra clase y que, por lo tanto, el conjunto está muy ordenado).
El valor máximo de la función anterior (es decir, la máxima impureza) en un escenario de clasificación binaria se alcanza cuando la proporción de cada muestra es igual a 0.50, en cuyo caso el índice Gini es igual a 1 - 0.52 - 0.52 = 0.5.
El valor máximo del índice Gini aumenta a medida que aumenta el número de clases. Así, por ejemplo, en un escenario con cuatro clases, la mayor impureza se daría cuando el número de muestras de cada clase fuese el mismo. Es decir, cuando la proporción de cada clase fuese igual a 0.25. En este caso, el índice Gini sería:
1 - 0.252 - 0.252 - 0.252 - 0.252 = 0.75