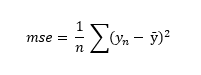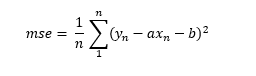Una vez involucrada una función de coste en el proceso de entrenamiento, el objetivo de cualquier algoritmo de Machine Learning pasa a ser el encontrar la configuración de los parámetros (en el caso de la Adaline, los valores de los pesos) que la minimice.
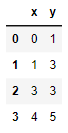
Veamos un sencillo ejemplo: Supongamos que partimos del siguiente conjunto de datos:
"x": [0, 1, 3, 4],
"y": [1, 3, 3, 5]
})
data
Si llevamos estos datos a un gráfico de dispersión podremos ver su distribución:
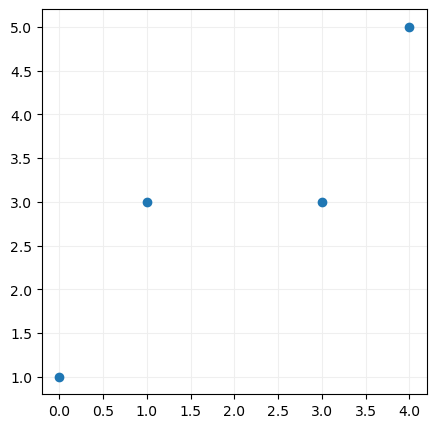
Supongamos ahora que queremos aproximar estos datos mediante una recta del tipo
Una vez decidamos los valores de los parámetros a y b, podremos medir el error cometido por nuestra recta según diferentes criterios. Por ejemplo, podríamos decantarnos por el llamado error cuadrático medio (mean squared error o MSE), definido como el valor medio de los cuadrados de la diferencia entre los valores predichos y los valores reales:
donde n es el número de puntos que estamos aproximando (4 en nuestro caso).
En este ejemplo, las predicciones ŷ vendrán dadas por la recta definida en [1], de forma que la función anterior podría rescribirse así:
Es decir, vemos que el error que nuestro modelo va a cometer depende -lógicamente- del valor que demos a los parámetros a y b que definen la recta. De esta forma, si escogemos, por ejemplo, los valores 0.1 y 1.5 para los parámetros a y b respectivamente, la recta quedaría del siguiente modo:
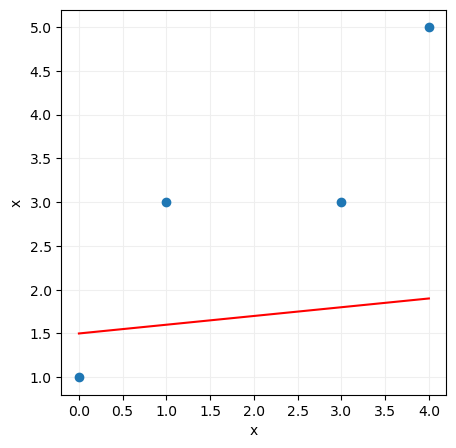
Si, por el contrario, damos a los parámetros a y b los valores 0.6 y 1.9, la recta anterior quedaría del siguiente modo:
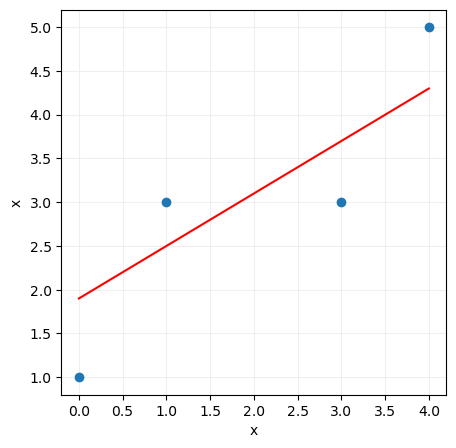
La primera recta calculada solo se aproxima razonablemente bien a uno de los puntos (al punto x = 0, y = 1) mientras que la segunda recta se aproxima bastante mejor a todos ellos. Esto nos hace presuponer que el error cometido va a ser menor en este segundo caso.
Podemos calcular a mano el error cuadrático medio en el primer caso:
mse
O podemos importar la función mean_squared_error de sklearn y dejar que sea ella quien calcule el error... Importamos la función:
Calculamos la predicción hecha por nuestra recta:
y_pred
1 2.5
2 3.7
3 4.3
Name: x, dtype: float64
Y calculamos el error cuadrático medio:
Salvo por el error de redondeo, las cifras obtenidas son iguales.
Calculemos entonces el mse correspondiente a la segunda recta creada:
y_pred = a * data.x + b
mean_squared_error(data.y, y_pred)
Valor mucho menor que el anterior.
La pregunta a hacerse entonces es cómo se pueden encontrar esos valores de los parámetros que aseguren que, dada una función de error, devuelven su valor mínimo.