Si quisiéramos formular matemáticamente este comportamiento, podríamos hacerlo fácilmente con las siguientes fórmulas:
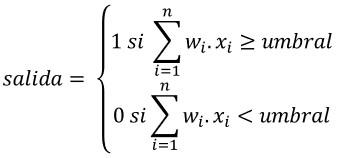
Es decir, cuando la suma de los productos de cada valor de entrada xi y el peso asociado wi sea mayor o igual que el umbral, la neurona devuelve un 1. En caso contrario devuelve un 0. Obsérvese que los sumatorios incluyen desde la señal de entrada 1 hasta la señal de entrada n.
Para simplificar, normalmente se pasa el umbral a la izquierda de la desigualdad con signo negativo:
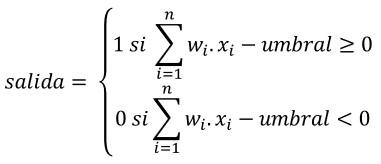
y a ese “-umbral” se renombra a b, quedando:
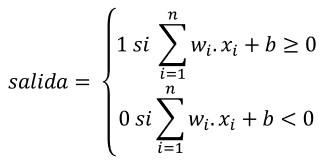
El término b es frecuentemente llamado bias.
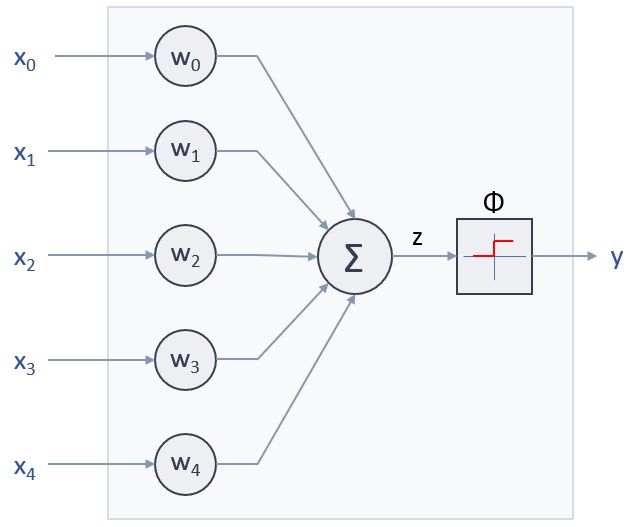
Ahora, el esquema de la neurona sería el siguiente:
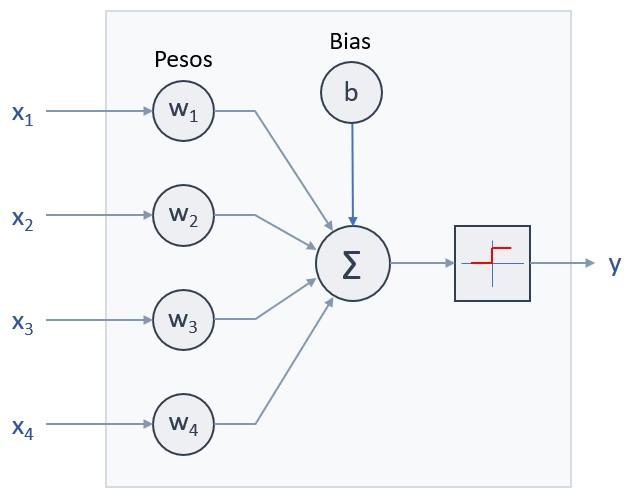
Obsérvese que, tras el cambio, la función de activación (la función escalón) está centrada en el valor 0.
De hecho, podemos ir más lejos y suponer que el bias, aun siendo un valor fijo (determinado durante la configuración de la neurona), es el valor de entrada x0, con un peso w0 igual a 1, en cuyo caso bastaría con modificar los sumatorios para que incluyesen también a esta “señal de entrada cero”:
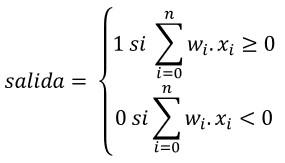
En este caso, el esquema del Perceptrón sería el siguiente:
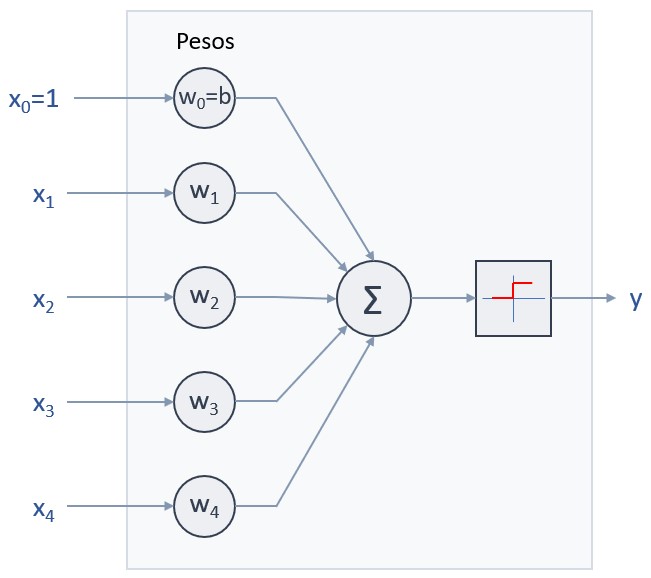
Si queremos simplificar aún más esta expresión, podemos considerar que el conjunto de pesos wi forman el vector fila w, y que el conjunto de valores xi forman el vector columna x, de forma que el sumatorio indicado puede obtenerse como el producto escalar de los vectores wT (el vector transpuesto de w) y x:
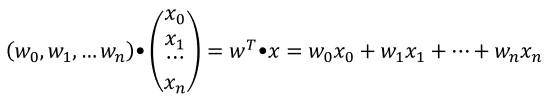
Es decir:
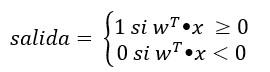
El resultado de la suma ponderada de los valores de entrada (lo que hemos formulado como wt●x) es lo que se conoce como net input (entrada neta en español) y frecuentemente se representa con la letra z. Por otro lado, también se suele usar el símbolo Φ para hacer referencia a la función de activación: