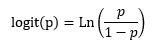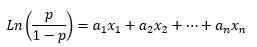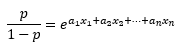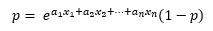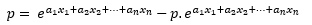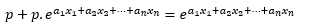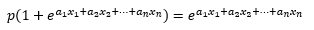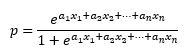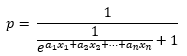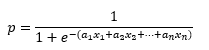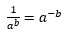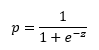Sin embargo, resulta obvio que, si el objetivo es predecir la probabilidad de un cierto evento, la relación entre las variables independientes mencionadas y la etiqueta (la probabilidad) no puede ser del tipo
entre otras cosas porque la probabilidad p va a tomar un valor en el rango [0, 1], mientras que nuestra combinación línea va a devolver valores potencialmente en el rango (-∞, +∞).
Para solucionar este problema no se considera la probabilidad a la izquierda de la igualdad en [2], sino la función logit que, aun involucrando la probabilidad p, tiene como rango (-∞, +∞). Esta función está definida de la siguiente forma:
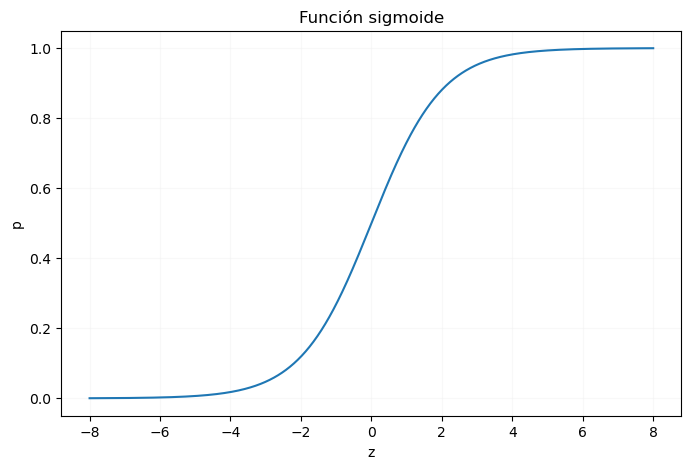
Si llevamos esta función a una gráfica, podemos ver su forma:
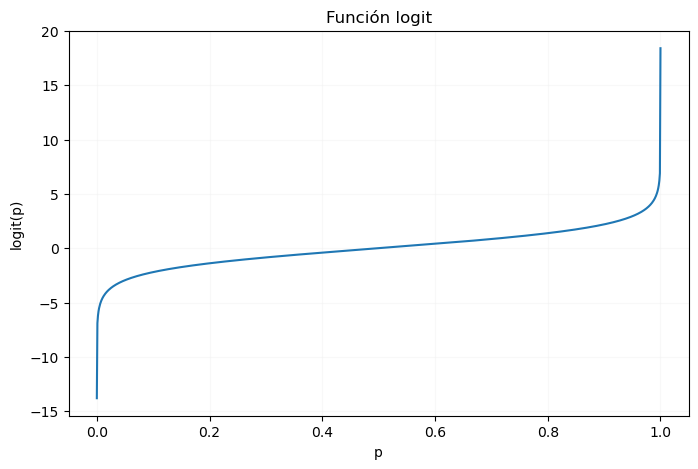
Es decir, nuestro modelo vendrá definido por la expresión
Como el objetivo es aproximar la probabilidad del evento, podemos extraer la variable p de la ecuación. Para ello obtenemos la exponencial de las expresiones a ambos lados de la igualdad:
Multiplicamos por (1 - p):
Multiplicamos la exponencial por los dos términos en el paréntesis:
Pasamos las probabilidades al lado izquierdo de la igualdad:
Sacamos p como factor común de la suma:
Y despejamos:
Esta expresión suele mostrarse tras dividir el numerador y el denominador por la exponencial:
O, lo que es lo mismo:
Por último, ya se ha comentado que a1x1 + a2x2 + ⋯ + anxn es lo que veníamos denominando net input o z, por lo que la ecuación queda finalmente de la siguiente forma:
Esta es la llamada función sigmoide y su aspecto es el siguiente: