Tal y como hemos visto, hay escenarios en los que resulta imposible evitar cometer una alta cantidad de errores en la clasificación. Fijémonos en las siguientes muestras, situadas en un espacio unidimensional:
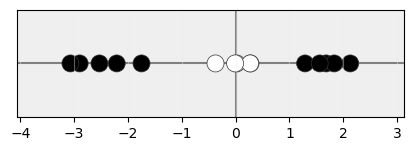
Si quisiéramos clasificar estas muestras en dos clases (blancas y negras), con independencia de dónde pusiéramos la frontera de decisión (el umbral o hiperplano de separación) siempre habría un número elevado de muestras mal clasificadas.
Supongamos ahora, sin embargo, que aplicamos a nuestros datos una función que los transforme en datos de un espacio de mayor dimensionalidad. Éstos ocupan inicialmente un espacio unidimensional, pero podríamos plantearnos el transformarlos a un espacio bidimensional en el que, por ejemplo, la coordenada x fuese la coordenada x original, pero la coordenada y fuese el cuadrado de la coordenada x. Tras la transformación nuestros datos tendrían la siguiente distribución:
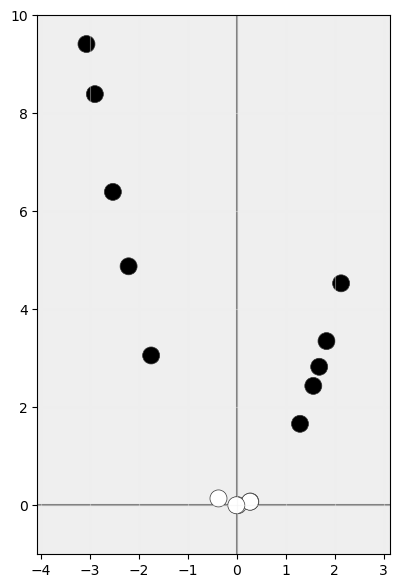
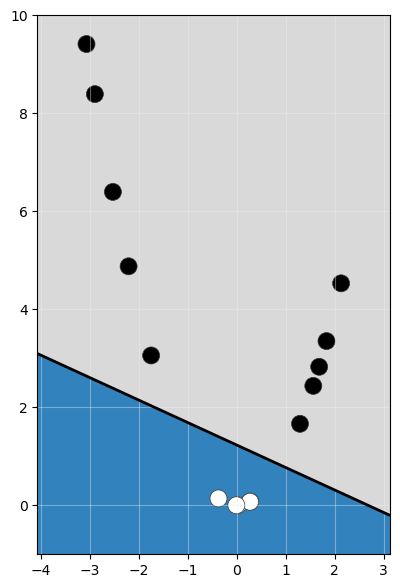
Ahora sí sería posible identificar un hiperplano que separe las muestras sin errores: