Todo algoritmo de Machine Learning se configura durante su entrenamiento. Una sencilla regresión lineal de la forma
se va a configurar determinando los valores de a y de b, los dos parámetros que la definen. La función de coste nos medirá la bondad del modelo final. Consideremos, por ejemplo, el error cuadrático medio:
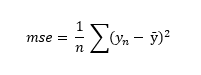
Este error nos dice que el error global que va a cometer el modelo vendrá dado por el valor medio de los cuadrados de las diferencias entre las predicciones y los valores reales. El hecho es que, siguiendo con el ejemplo de regresión lineal comentado, para cada par de valores de a y b que puedan determinarse durante el entrenamiento tendremos un error cuadrático medio diferente. El objetivo del entrenamiento parece entonces claro: encontrar los valores de a y b que minimicen la función de coste. La pregunta es obligada: ¿cómo encontramos los valores de los parámetros (a y b en nuestro ejemplo) que minimizan esa función de coste? Si la función de coste es sencilla y el conjunto de datos a entrenar no es excesivamente grande, podemos recurrir al cálculo infinitesimal para el cálculo del mínimo de la función. De hecho, en el caso de una función lineal como la comentada, hay una fórmula (la llamada "ecuación normal") que nos devuelve los valores de los parámetros que minimizan la función.
El problema es que, normalmente, el cálculo de los parámetros que minimizan una cierta función de coste aplicando cálculo infinitesimal puede resultar computacionalmente inabordable. En una red neuronal, por ejemplo, podemos tener cientos de miles de pesos y de "bias", elementos cuyos valores hay que determinar durante el entrenamiento de la red neuronal para que ésta pueda realizar predicciones precisas. Es por ello que se suele recurrir a algoritmos como el descenso de gradiente para el cálculo de estos mínimos. Pero, por supuesto, aplicar el algoritmo de descenso de gradiente implica el cálculo del gradiente de la función de coste en un punto concreto de su dominio (en un punto determinado por unos parámetros concretos), lo que a su vez implica el cálculo de la derivada parcial de la función de coste con respecto a todos y cada uno de los parámetros que van a determinar el funcionamiento de la red.
Ahora imaginemos una red neuronal de decenas de capas ocultas, con miles o decenas de miles de neuronas artificiales en cada una de ellas, escojamos una neurona cualquiera de una capa cualquiera, y uno de los enlaces que le llegan desde una neurona de la capa anterior. Ese enlace viene caracterizado por un peso que, en mayor o menor grado, va a determinar el comportamiento de la red. Y minimizar el error de la red (minimizar la función de coste) implica determinar el valor correcto de ese peso (y del resto de miles de pesos y bias comentados). ¿Cuál es la derivada parcial de la función de coste con respecto a dicho peso? Ese peso va a influir en el resultado devuelto por la neurona que habíamos escogido, lo que influirá a su vez en los resultados que devolverán las neuronas de la siguiente capa... El cálculo de la derivada parcial de la función de coste con respecto a dicho peso no parece una tarea fácil.
En el pasado se utilizaban métodos que, basados en la fuerza bruta, estimaban la derivada parcial en cuestión, modificando el valor del peso y viendo el efecto que tenía en la salida de la red, pero esto, además de ser poco fiable, era computacionalmente muy caro.