Y es aquí donde el algoritmo de backpropagation (o "retropropagación") llega para resolver el problema. Sin querer entrar en profundidad en las matemáticas que hay por detrás de este algoritmo, veamos un ejemplo muy simple. Supongamos la siguiente red formada por dos capas ocultas con una única neurona artificial en cada una:
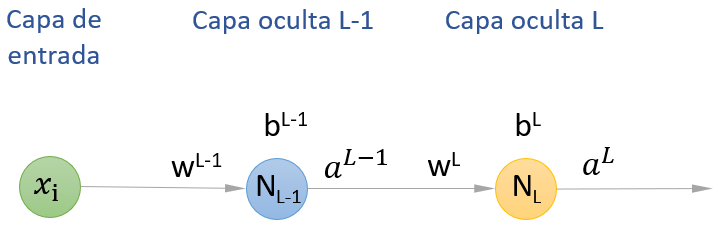
Vamos a llamar a la segunda capa oculta (la más próxima a la salida de la red) L y a la primera capa oculta, L-1.
El comportamiento de la neurona artificial de la capa L (la neurona NL) viene determinado por el peso del enlace que la une con el valor devuelto por la capa anterior, wL, y por el bias a añadir, bL.¿Cómo calcularíamos, por ejemplo, la derivada parcial de la función de coste con respecto a estos dos parámetros, wL y bL?:
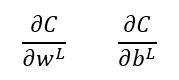
En estas expresiones, C es la función de coste, resultante de analizar el comportamiento de la red neuronal con todas las muestras del conjunto de entrenamiento. Para una de las muestras, la i-ésima, las expresiones anteriores vendrían dadas por:
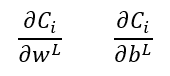
pudiendo calcularse el coste C como el valor medio de los valores Ci obtenidos para todas las muestras.
Supongamos que la función de coste viene dada por el error cuadrático medio ya comentado:
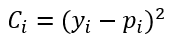
En esta expresión yi es el valor que debería devolver la red para la muestra i-ésima (es decir, la etiqueta asociada a dicha muestra) y pi es el valor que en realidad devuelve la red para la muestra en cuestión (la predicción). Este valor pi viene dado, como ya sabemos, por la multiplicación del valor devuelto por la neurona anterior por peso del enlace, más el bias, y pasando el resultado de esta combinación lineal por la función de activación, que podemos llamar σ:
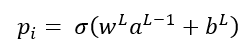
Es decir, la función de coste puede expresarse también como:
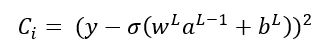
Por comodidad, llamemos zL a la combinación lineal wLaL-1 + bL:
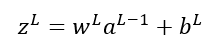
De forma que:
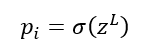
Pues bien, el cálculo infinitesimal nos dice que la derivada de la función Ci con respecto a wL (es decir, cómo varía Ci cuando variamos wL) coincide con la derivada de Ci con respecto a σ, multiplicado por la derivada de σ respecto de zL, multiplicado por la derivada de zL con respecto a wL. Esto es lo que se llama regla de la cadena:
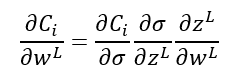
La buena noticia es que todas estas derivadas parciales son fácilmente calculables:
- La derivada parcial de Ci con respecto a σ es, para la función de coste escogida, 2(y-σ).
- La derivada parcial de σ con respecto a zL es la derivada de la función de activación con la que estemos trabajando.
- La derivada parcial de zL con respecto a wL es aL-1.
De modo análogo, la derivada parcial de Ci con respecto al bias bL vendría dada por una expresión semejante a la anterior:
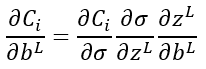
lo que resulta, incluso, más fácil de calcular, pues la derivada parcial de zL con respecto a bL es 1.
Sin entrar más profundamente en las matemáticas, el hecho es que aplicando la regla de la cadena, podemos ir desde atrás hacia delante (desde la función de coste expresada en función de los valores devueltos por la capa de salida hacia las primeras capas) calculando las derivadas parciales de la función de coste con respecto a todos los pesos y los bias. A medida que vamos calculando derivadas parciales, las de la capa oculta a calcular a continuación (capa más próxima a la entrada de la red, pues recordemos que estamos yendo de atrás adelante) hará uso de las derivadas parciales ya calculadas, por lo que el cálculo del gradiente resulta relativamente sencillo.
Este algoritmo es el que permite el cálculo del gradiente en cualquier punto del dominio de la función de coste y, por lo tanto, el que permite el cálculo del mínimo de la función de coste, objetivo del entrenamiento.