Importamos ahora la clase MLPClassifier e instanciamos el algoritmo:
from sklearn.neural_network import MLPClassifier
(2, ),
random_state = 0,
learning_rate_init = 0.1,
activation = "logistic"
)
Estamos creando el modelo con una tasa de aprendizaje de 0.1, especificando como función de activación de las capas ocultas la función logística (o sigmoide). Entrenamos ahora el modelo:
El objeto instanciado tiene dos atributos que nos dan acceso a los coeficientes y a los interceptores:
model.coefs_
[array([[-0.14736599, -1.15400831],
[-7.83405221, 9.72328823]]),
array([[-6.60705046],
[ 6.00857268]])]
model.intercepts_
[array([ 3.89827002, -4.41150649]), array([0.20379602])]
El atributo .coefs_ devuelve un array con tantos elementos como capas (excluyendo la de entrada que ya se ha comentado que no va a aplicar ninguna transformación a los datos), estando formado cada elemento del array por una matriz de coeficientes (de pesos).
El atributo .intercepts_ devuelve otro array en el que cada elemento contiene el vector de bias de la capa correspondiente.
Ahora podemos llevar estos valores (redondeados) a nuestro esquema con la estructura de la red neuronal que acabamos de crear:
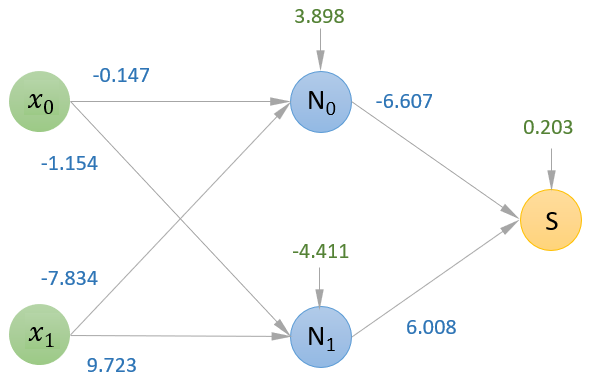
(se muestran en azul los coeficientes y en verde los bias).
Una vez entrenada la red, para realizar una predicción, por ejemplo para el valor (x0 = 0.8, x1 = 0.3), bastaría con hacer pasar dicho valor por la red, aplicándose las funciones vistas en cada nodo (obtención de la entrada neta y paso de ésta por la función sigmoidea), hasta alcanzar la capa de salida. La neurona artificial de esta capa de salida (solo una en el caso de clasificación binaria) aplica una función sigmoidea (con independencia de la función de activación usada en el resto de la red) al dato que resulta de ponderar y sumar sus datos de entrada y su bias, convirtiendo dicho dato en una probabilidad y deduciendo, a partir de ella, la clase a asignar.
